Déanann an leathanach seo cur síos ar bhunghnéithe an Mhéadaithe agus ar na cineálacha céimnithe i gcumarsáid gan sreang. Roinntear na cineálacha céimnithe ina chéimniú mórscála agus céimniú beagscála (leathadh moille ilchonaire agus scaipeadh doppler).
Is cuid de chéimniú ilchonair iad céimniú cothrom agus céimniú roghnúcháin minicíochta ach is cuid de chéimniú scaipthe Doppler iad céimniú tapa agus céimniú mall. Cuirtear na cineálacha céimnithe seo i bhfeidhm de réir dáiltí nó samhlacha Rayleigh, Rician, Nakagami agus Weibull.
Réamhrá:
Mar is eol dúinn, is éard atá i gcóras cumarsáide gan sreang ná tarchuradóir agus glacadóir. Níl an cosán ón tarchuradóir go dtí an glacadóir réidh agus féadfaidh an comhartha tarchurtha dul trí chineálacha éagsúla maoluithe, lena n-áirítear cailliúint cosáin, maolú ilchonaire etc. Braitheann maolú an chomhartha tríd an gcosán ar fhachtóirí éagsúla. Is iad sin am, minicíocht raidió agus cosán nó suíomh an tarchuradóra/ghlacadóra. Is féidir leis an gcainéal idir an tarchuradóir agus an glacadóir a bheith athraitheach ó thaobh ama de nó seasta ag brath ar cibé an bhfuil an tarchuradóir/glacadóir seasta nó ag bogadh i leith a chéile.
Cad atá ag céimniú?
Tugtar céimniú ar an athrú ama ar chumhacht an chomhartha a fhaightear mar gheall ar athruithe sa mheán tarchuir nó sna cosáin. Braitheann an céimniú ar fhachtóirí éagsúla mar a luadh thuas. I gcás seasta, braitheann an céimniú ar dhálaí atmaisféaracha amhail báisteach, tintreach etc. I gcás soghluaiste, braitheann an céimniú ar chonstaicí ar an gcosán atá ag athrú i leith ama. Cruthaíonn na constaicí seo éifeachtaí casta tarchuir don chomhartha tarchuir.
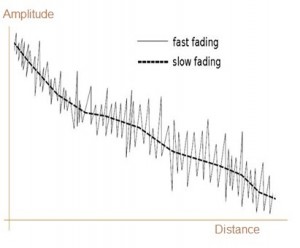
Léiríonn figiúr-1 cairt aimplitiúid i gcoinne achair do chineálacha céimnithe mall agus céimnithe tapa a phléifimid níos déanaí.
Cineálacha céimnithe
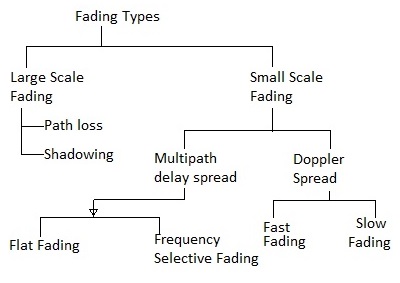
Agus laguithe éagsúla a bhaineann le cainéil agus suíomh an tarchuradóra/glacadóra á mbreithniú, seo a leanas na cineálacha céimnithe i gcóras cumarsáide gan sreang.
➤Céimniú ar Scála Mór: Áirítear leis cailliúint cosáin agus éifeachtaí scáthaithe.
➤Céimniú Beag: Tá sé roinnte ina dhá phríomhchatagóir eadhon, scaipeadh moille ilchonaire agus scaipeadh doppler. Tá an scaipeadh moille ilchonaire roinnte ina chéimniú comhréidh agus céimniú roghnach minicíochta. Tá scaipeadh doppler roinnte ina chéimniú tapa agus céimniú mall.
➤Samhlacha céimnithe: Cuirtear na cineálacha céimnithe thuas i bhfeidhm i samhlacha nó i ndáiltí éagsúla lena n-áirítear Rayleigh, Rician, Nakagami, Weibull etc.
Mar is eol dúinn, tarlaíonn comharthaí meathlaithe mar gheall ar fhrithchaitheamh ón talamh agus ó fhoirgnimh máguaird chomh maith le comharthaí scaipthe ó chrainn, daoine agus túir atá i láthair i limistéar mór. Tá dhá chineál meathlaithe ann eadhon meathlú ar scála mór agus meathlú ar scála beag.
1.) Céimniú ar Scála Mór
Tarlaíonn céimniú mórscála nuair a thagann constaic idir an tarchuradóir agus an glacadóir. Is cúis le laghdú suntasach ar neart an chomhartha an cineál seo cur isteach. Tá sé seo amhlaidh toisc go mbíonn scáth nó bac ar thonnta EM ag an gconstaic. Tá baint aige le luaineachtaí móra sa chomhartha thar achar.
1.a) Cailliúint cosáin
Is féidir an caillteanas cosáin spáis shaor a chur in iúl mar seo a leanas.
➤ Pt/Pr = {(4 * π * d)2/ λ2} = (4*π*f*d)2/c2
Cá háit,
Pt = Cumhacht tarchuir
Pr = Cumhacht a fháil
λ = tonnfhad
d = an fad idir antenna tarchuir agus glactha
c = luas an tsolais i.e. 3 x 108
Ón gcothromóid, tugann sé le fios go maolaíonn an comhartha tarchurtha le fad de réir mar a scaiptear an comhartha thar achar níos mó agus níos mó ón taobh tarchurtha i dtreo an taobh glactha.
1.b) Éifeacht scáthaithe
• Breathnaítear air i gcumarsáid gan sreang. Is éard atá i scáthú ná diall chumhacht a fhaightear ó chomhartha EM ón meánluach.
• Is toradh é ar bhacainní ar an gcosán idir an tarchuradóir agus an glacadóir.
• Braitheann sé ar shuíomh geografach chomh maith le minicíocht raidió tonnta EM (Leictrea-Maighnéadacha).
2. Céimniú ar Scála Beag
Baineann céimniú beag le luaineachtaí gasta i neart an chomhartha a fhaightear thar achar an-ghearr agus thar thréimhse ghearr ama.
Bunaithe arscaipeadh moille ilchonairTá dhá chineál céimnithe beagscála ann, eadhon céimnithe comhréidh agus céimnithe roghnach minicíochta. Braitheann na cineálacha céimnithe ilchonaire seo ar an timpeallacht iomadúcháin.
2.a) Céimniú cothrom
Deirtear go bhfuil céimniú comhréidh ar an gcainéal gan sreang má tá gnóthachan tairiseach agus freagairt chéime líneach aige thar bhandaleithead atá níos mó ná bandaleithead an chomhartha tarchurtha.
Sa chineál seo céimnithe, luainíonn comhpháirteanna minicíochta uile an chomhartha a fhaightear sna comhréireanna céanna ag an am céanna. Tugtar céimnithe neamhroghnach air freisin.
• Comhartha BW << Cainéal BW
• Tréimhse siombail >> Moill Scaipeadh
Feictear éifeacht an chéimnithe chomhréidh mar laghdú ar an SNR. Tugtar bealaí athraitheacha aimplitiúide nó bealaí caolbhanda ar na bealaí céimnithe chomhréidh seo.
2.b) Céimniú Roghnach Minicíochta
Bíonn tionchar aige ar chomhpháirteanna speictreacha éagsúla de chomhartha raidió le haimplitiúidí éagsúla. Dá bhrí sin an t-ainm céimniú roghnach.
• Comhartha BW > Cainéal BW
• Tréimhse siombaile < Moill Scaipeadh
Bunaithe arscaipeadh dopplerTá dhá chineál céimnithe ann, eadhon céimnithe tapa agus céimnithe mall. Braitheann na cineálacha céimnithe scaipthe Doppler seo ar luas soghluaiste i.e. luas an ghlacadóra i gcomparáid leis an tarchuradóir.
2.c) Ag céimniú go tapa
Léirítear feiniméan an mheathlaithe thapa trí luaineachtaí meara comhartha thar limistéir bheaga (i.e. bandaleithead). Nuair a thagann na comharthaí ó gach treo sa phlána, breathnófar meathlú tapa i ngach treo gluaiseachta.
Tarlaíonn céimniú tapa nuair a athraíonn freagairt impulse cainéil go han-tapa laistigh de ré an tsiombail.
• Scaipeadh ard-doppler
• Tréimhse siombail > Am comhtháthaithe
• Éagsúlacht Comhartha < Éagsúlacht cainéil
Is é an toradh a bhíonn ar na paraiméadair seo ná scaipeadh minicíochta nó céimniú roghnach ama mar gheall ar scaipeadh Doppler. Is toradh ar fhrithchaitheamh rudaí áitiúla agus gluaiseacht rudaí i gcoibhneas leis na rudaí sin é céimniú tapa.
I gcéimniú tapa, is suim comharthaí iomadúla a fhrithchaitheann ó dhromchlaí éagsúla an comhartha glactha. Is suim nó difríocht comharthaí iolracha an comhartha seo, agus is féidir leo a bheith tógálach nó millteach bunaithe ar an aistriú céime coibhneasta eatarthu. Braitheann caidrimh chéime ar luas gluaiseachta, minicíocht tarchuir agus faid choibhneasta na gcosán.
Saobhadh céimnithe tapa cruth na cuisle bonnbhanda. Tá an saobhadh seo líneach agus cruthaíonn séISI(Cur isteach idir Shiombailí). Laghdaíonn cothromú oiriúnaitheach ISI trí shaobhadh líneach a spreagann an cainéal a bhaint.
2.d) Ag céimniú go mall
Is toradh scáthú ó fhoirgnimh, cnoic, sléibhte agus rudaí eile ar an gcosán é céimniú mall.
• Scaipeadh Doppler Íseal
• Tréimhse siombail <
• Éagsúlacht Comhartha >> Éagsúlacht Cainéal
Cur i bhfeidhm samhlacha céimnithe nó dáiltí céimnithe
I measc na gcur i bhfeidhm de shamhlacha céimnithe nó dáiltí céimnithe tá céimniú Rayleigh, céimniú Rician, céimniú Nakagami agus céimniú Weibull. Tá na dáiltí nó na samhlacha cainéil seo deartha chun céimniú a ionchorprú sa chomhartha sonraí bonnbhanda de réir riachtanais phróifíl an chéimnithe.
Rayleigh ag céimniú
• I samhail Rayleigh, ní dhéantar ach comhpháirteanna Neamh-Líne Radharc (NLOS) a insamhladh idir an tarchuradóir agus an glacadóir. Glactar leis nach bhfuil aon chonair LOS ann idir an tarchuradóir agus an glacadóir.
• Soláthraíonn MATLAB feidhm "rayleighchan" chun samhail chainéil Rayleigh a insamhladh.
• Tá an chumhacht dáilte go heaspónantúil.
• Tá an chéim dáilte go haonfhoirmeach agus neamhspleách ar an aimplitiúid. Is í an cineál céimnithe is mó a úsáidtear i gcumarsáid gan sreang í.
Imeacht Ríceach
• I samhail na Stát Aontaithe, déantar comhpháirteanna Líne Radharc (LOS) agus neamh-Líne Radharc (NLOS) a insamhladh idir an tarchuradóir agus an glacadóir.
• Soláthraíonn MATLAB feidhm "ricianchan" chun samhail chainéil rician a insamhladh.
Nakagami ag céimniú
Is samhail staitistiúil í cainéal céimnithe Nakagami a úsáidtear chun cur síos a dhéanamh ar bhealaí cumarsáide gan sreang ina dtéann an comhartha a fhaightear faoi chéimniú ilchonair. Léiríonn sé timpeallachtaí a bhfuil céimniú measartha go dian orthu amhail ceantair uirbeacha nó fo-uirbeacha. Is féidir an chothromóid seo a leanas a úsáid chun samhail cainéal céimnithe Nakagami a insamhladh.

• Sa chás seo, léirítear h = r*ejΦagus tá uillinn Φ dáilte go haonfhoirmeach ar [-π, π]
• Glactar leis go bhfuil an athróg r agus Φ neamhspleách ar a chéile.
• Tá an pdf Nakagami léirithe mar atá thuas.
• Sa pdf Nakagami, 2σ2= E{r2}, is é Γ(.) an fheidhm Gamma agus is é k >= (1/2) an figiúr céimnithe (céimeanna saoirse a bhaineann le líon na n-athróg randamacha Gauss a cuireadh leis).
• Forbraíodh é ar dtús go heimpíreach bunaithe ar thomhais.
• Tá cumhacht glactha meandrach dáilte le gama. • Le k = 1 Rayleigh = Nakagami
Weibull ag céimniú
Is samhail staitistiúil eile í an cainéal seo a úsáidtear chun cur síos a dhéanamh ar chainéal cumarsáide gan sreang. Úsáidtear cainéal céimnithe Weibull go coitianta chun timpeallachtaí a léiriú ina bhfuil cineálacha éagsúla coinníollacha céimnithe, lena n-áirítear céimniú lag agus céimniú dian araon.

Cá háit,
2σ2= E{r2}
• Léiríonn dáileadh Weibull ginearálú eile ar dháileadh Rayleigh.
• Nuair a bhíonn X agus Y ina n-athróga Gaussacha meán nialasacha, is é clúdach R = (X2+ Y2)1/2an bhfuil dáileadh Rayleigh air. • Mar sin féin, sainmhínítear an clúdach R = (X2+ Y2)1/2, agus is é an pdf comhfhreagrach (próifíl dáilte cumhachta) atá dáilte ag Weibull.
• Is féidir an chothromóid seo a leanas a úsáid chun samhail céimnithe Weibull a insamhladh.
Ar an leathanach seo, phléamar ábhair éagsúla faoi chéimniú amhail cad is cainéal céimnithe ann, a chineálacha, samhlacha céimnithe, a bhfeidhmeanna, a bhfeidhmeanna agus araile. Is féidir an fhaisnéis ar an leathanach seo a úsáid chun comparáid a dhéanamh idir céimniú beagscála agus céimniú mórscála agus an difríocht idir céimniú comhréidh agus céimniú roghnach minicíochta a dhíorthú, an difríocht idir céimniú tapa agus céimniú mall, an difríocht idir céimniú Rayleigh agus céimniú California agus araile.
E-mail:info@rf-miso.com
Fón: 0086-028-82695327
Suíomh Gréasáin: www.rf-miso.com
Am an phoist: 14 Lúnasa 2023







